本文目录
文章大致来源:
问题背景:
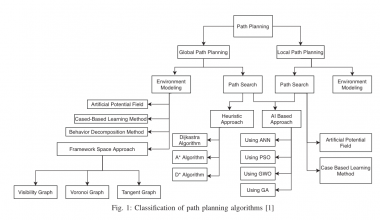
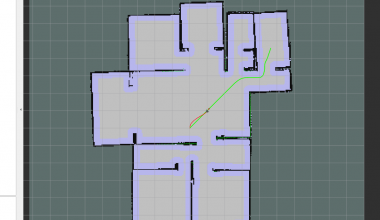
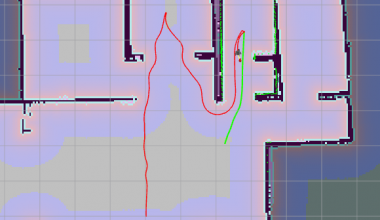
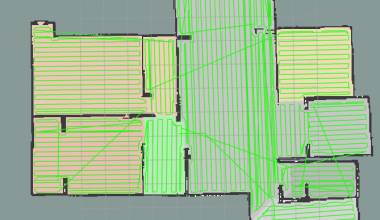
机器人通过栅格地图进行路径规划时,根据静态障碍物得到全局路径。通过各种路径规划算法,如 Dijkstra's,A*,D-star,RRT等,规划出的路径都存在直线之间有急剧拐弯(曲率变化大)的问题,对于实际机器人是没办法连续完成这样的路径的,大多需要停止运动转向继续行驶,这样的话能量消耗较大且工作效率较低。针对这个问题就需要对寻找到的路径进行平滑处理。
解决思路:
将路径修改为各段各点间 ①速度 ②加速度 ③曲率 三部分连续
优化方法:
- 多项式插值
插值法用于路径平滑十分原始,有两个缺点:①计算复杂度高;②Runge's 现象;
(Runge's现象为龙格现象,即随着插值节点个数增加,反而不能更好地逼近被插值函数的现象。理论了解:函数逼近——拉格朗日插值下的(Runge)龙格现象 | 北太天元 or matlab )
对于路径优化的应用:平滑轨迹插值方法之多项式插值(附代码) - 贝塞尔曲线
贝塞尔曲线是应用于二维图形应用程序的数学曲线,由一组称为控制点的向量来确定,给定的控制点按顺序连接构成控制多边形,贝塞尔曲线逼近这个多边形,进而通过调整控制点坐标改变曲线的形状。控制点的作用是控制曲线的弯曲程度理论了解:详解样条曲线(上)(包含贝塞尔曲线)
对于路径优化的应用:【路径规划】局部路径规划算法——贝塞尔曲线法(含python实现 | c++实现) - 三次样条曲线
理论了解:基于三次样条插值的路径规划算法
对于路径优化的应用: - B样条曲线
理论了解:详解样条曲线(上)(包含贝塞尔曲线)
对于路径优化的应用:基于B-spline的轨迹优化 - NURBS 曲线
理论了解:
对于路径优化的应用: - Dubin's曲线
理论了解:
对于路径优化的应用: - Clothoid曲线
理论了解:
对于路径优化的应用: - Hypocycloid
理论了解:
对于路径优化的应用: - Reeds-Shepp Curves
理论了解:
对于路径优化的应用: - Balkcom-Mason 曲线
理论了解:
对于路径优化的应用: